回路にだまされないために

非なるが同じ回路

「似て非なるもの」という言葉があるので、反対に　「非なるが似ているもの、同じモノ」　というのも探せばあるのでしょう。

 

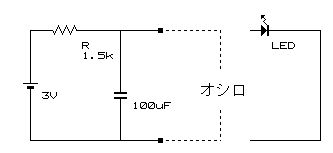
この回路は　「コンデンサを試す」　に出てきた回路です。

 

ディレイ機能をもつディレイ回路と紹介しました。

 

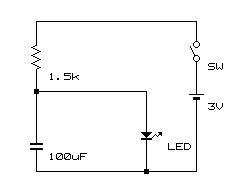
しかし、あんまり遅れず、一瞬遅くなる回路でした。

積分回路

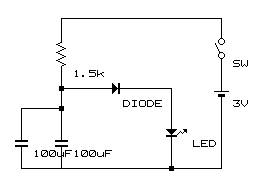
この回路も横にして書き換えると、こうなります。（これも書き方が違うだけで上と全く同じ回路です）

 

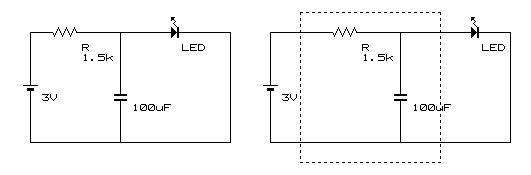
この右側の回路、点線で囲んだ部分をみると、回路の教科書などの基礎回路の説明に一度は出てくる、「積分回路」というものです。

（「積分回路」と言う名前が難しそうで、積分の作用をするという風に考えず、そんな名前と思っておきましょう。）

遠目に眺めると、普通に直接、電池にＬＥＤだけつないだ回路の途中に　この「積分回路」が入っているだけの回路です。

 

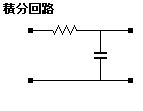
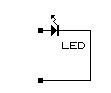
実際にコンデンサを”自動的に変わる抵抗”と　とらえて、ＬＥＤディレイ回路といったこの回路は、形を変えると「積分回路」を通してＬＥＤにつないでいるだけです。。。。

 

ディレイ作用はこの「積分回路」がやってるだけです。

 

上の真ん中のブロック（積分回路）を省いてＬＥＤにつなぐと、単純にＬＥＤが点灯する回路です。

 

積分回路の動作

どんな動作をするか？

では、ラインの間に、この「積分回路」を割り込ませるとどうなるか？

 

結局、「積分回路」が何をするかということになります。

その電圧の上がり方は、対数曲線に似ているので、この関数で近似されます。

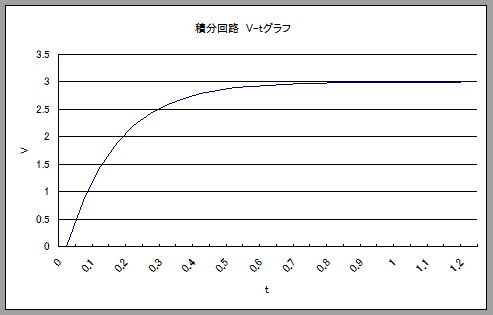
関数でわざわざ表すとなにが便利かというと、実験しなくても動作がわかる。この曲線をみていると、コンデンサに通電したときの電圧の上昇の仕方がよくわかります。

 

最初はグッと上昇し、その後は緩やかに上昇なかなか伸びず、満タンになるまで○○秒と。
コンデンサを試す　の最初の実験回路では、遅れが小さすぎ、遅れがあるかどうかわからない程度でしたが、

• どのくらい遅れるのか？
• コンデンサの容量を増やすと遅れ時間はどのぐらい増えるか？

感覚と実験で試して容量を増やすなどしてやってみました。

楽しく実験しながら回路の動作を調べていくのも大事ですが、抵抗値やコンデンサ容量を次々変えて実験する方法ばかりでは「工作」　の領域を出ません。

回路の動作を計算する

これを数学的に式でとらえて計算したり解析することにより、回路の動作をとらえることができます。

 

本当に計算でディレイ時間がわかるのか？

本当に対数関数を持ち出せば、”プルアップのナゾ”　からつながったこの回路がわかるのでしょうか？

　コンデンサを２つ付け容量を倍にしたり、ダイオードを挟んだりしてディレイさせましたが、どこをどうすれば、どれだけ効果がでるのでしょう？

 

回路のグラフ

「積分回路」のグラフ、このグラフを見たり、計算式からたどります。

 

 

積分回路の電圧計算式

Vc = V[1-e^-(t/CR)]

 

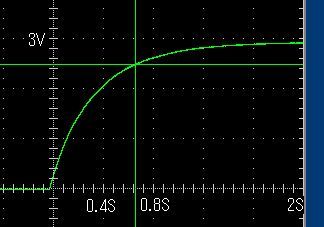
グラフを読むと

V=３　　つまり　「満タン」３Vまでｔ＝１ぐらい　

しかし

V=１．５　半分　つまり　「半タン」までは約　t=０．１５　程度の時間でたどり着いています。

 

スタートは全速で飛ばすが、真ん中から駆け足、終盤はゆっくり歩くマラソン選手のようなゴールへの道です。

 

終盤はゆっくり、じれったく上がるのが積分回路の動作とわかります。

計算式

計算式を使ってみます。

この積分回路の計算式は

 

Vc = V[1-e^-(t/CR)] 　で表されます

 

計算式を実験

実験した回路を当てはめてみます。

 

スイッチをつなげて　０．１5秒後には　何ボルトになっているのでしょうか？
各部品の数値を放り込み、0.1５秒後には何Vになるか

ディレイ（遅れ）しなかった回路で計算

 

この数値データをこの式に放り込むと
　　Vc=３V　×（１－０．３６８）=１．９V

 

結果はわずかt=0.15:0.15秒後には約1.9Vになります。

 

1.9Vをグラフで読み取ると

ＬＥＤは約１．８Ｖ程度になれば点灯するので、0.15秒も待たず（ディレイ）せずにＬＥＤが点灯することがわかります。

 

ディレイ（遅れ）した回路で計算

次に、コンデンサを試す　で登場した、

遅れがハッキリ実感できた改良型のディレイ回路でt=0.5で計算してみると

 

 

Vc=3V×(1-0.188) =2.44V　になります。

 

ダイオードを間に入れて、ＬＥＤが1.8Vで点灯するところを　1.8V+0.7V=2.5Vとしていいるので

約2.44Vまで上昇する時間が、計算から0.5秒、約2.5V程度でＬＥＤは点灯するので
この改良型のディレイ回路の遅れは約0.5秒。
これなら人の目にも遅れがハッキリ実感できたわけです。

 

しかし、本当に計算した遅れ時間になっているのでしょうか？

計算式を実験する

積分回路の計算式が実際はどのようになるのか？

積分回路の動作を実際に回路で動かしてみます。

 

それでは実験しときましょう。。。。と、いつも通りいきたいのですが、
目をこらしてＬＥＤを見つめ、点灯するまでの0.1秒や0.2秒を正確に測るのは、ナンボなんでも苦しいです！　

今回は、デジタルオシロスコープを使えば全部解決
デジタルオシロは単発現象も記録できるので、電圧がどのような変化をするかグラフのようにして記録出来ます。

 

最初の積分回路の電圧上昇を実験

計算式１

ＬＥＤをどけて、オシロスコープで観察したＬＥＤへの電圧を見てみます。　

 

 

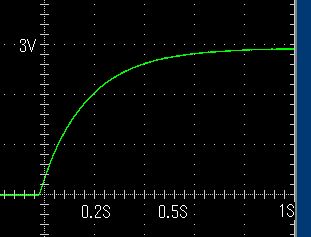
計算式では0.15秒後の電圧は　
t=0.15[s]　　Vc=３V　×（１－０．３６８）=１．９V　になりました。
（数式のグラフとほぼ一致）

実測の電圧の上昇を見ると、少し違いはありますが、だいたい合っています。
上昇のしかたもホントに対数関数と同じなのがわかります。

コンデンサ容量を２倍にして実験

コンデンサを並列に置き容量を２倍にしてみます

 

 

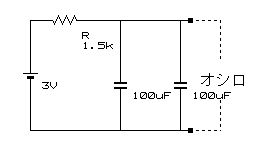
コンデンサ容量を２倍にすると
時間が２倍になり、時間スケールを２倍に変えただけで形はほとんど変わらず、計算式のｔとCの関係がそのままでています。

計算式から求めた結果は

かなりそのまま実際の回路でも同じになり、計算式でも動作の予測を立てられることがわかります。