ホイートストンブリッジ
高校で勉強する、おなじみのホイートストンブリッジとはこういう回路です。
ホイートストンブリッジ回路
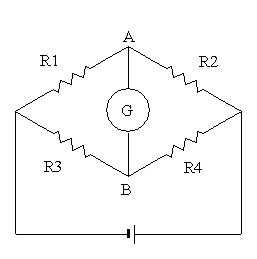
ひずみゲージの回路の例としてよく取り上げられます。
実際、回路図に入り、実用回路の中にこの回路に似たような回路は出てこないかと、ヒシ形を待ち構えていても、おそらく一生こんなヒシ形の回路に出会うことはないでしょう。
ここでせっかく勉強して習ったホイートストンブリッジを考えてみます。
ホイートストンブリッジの原理
まず、回路図でこのような2本の並列接続の回路を考えます。コンデンサを試す に出てきた分圧回路2個分です
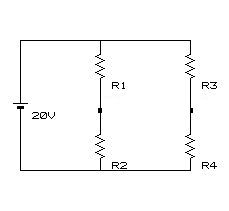
並列接続では電圧が一定となるので、
縦の2本の線は別々の回路のように考えることができます。
各縦線の並列回路の抵抗の電流、電圧は、
「コンデンサを試す」のところの計算ででます。
この真ん中をつないでみたらどちら向きに電流が流れる?
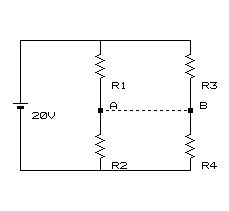
この間をつないだら?
というのがホイートストンブリッジです。
さて、こういう抵抗値にしてみて、つないでみたら、
- どちら向きに電流が流れるでしょうか?
- 電流が流れないときはどんな抵抗値のときか?
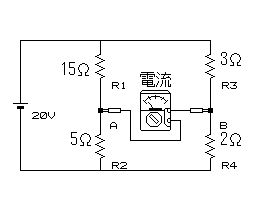
*これは例題の回路です
というのが ホイーストンブリッジの問題です
A点とB点の電圧は コンデンサを試す の 分圧のところであったように
A点
| 20V | × | 5 15+5 |
=5V
B点
| 20V | × | 2 3+2 |
=8V
この2点の電圧を較べればいいのです。
つないだ橋渡しのラインに電流が流れない条件は
各抵抗が
| R1 R3 | = | R2 R4 |
になる というのがホイーストンブリッジの公式です。
この均衡が崩れると、どちら向きかに電流が流れることになります。
その方向は A点 B点 の電圧の高い方から低い方に流れます。
橋渡しの部分の電圧を測れば、微妙な曲がりでも、たわんだ変化が電圧となってわかるという原理です
並列接続間の電圧
A点とB点の電圧は >コンデンサを試す の 分圧のところであったように
この回路なら

- A点電圧 5V
- B点電圧 8V
となり B点→A点 へ流れます。
しかし、橋渡しの間を たとえば 抵抗:R5 でつないだとき、
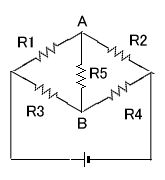
そこに流れる電流は
| I | = | VB-VA R5 |
とは簡単には計算できません
これは、実は 分圧の式のようなものでは簡単には求まりません。
電位差を流れる電気
電流や電圧を厳密に計算するより、 ホイーストンブリッジの重要な点は、
圧力が均衡すると、道はあっても電気は流れない ということです。
ホイーストンブリッジが教えてくれる重要なことの1つは
電気は + → グランド へ流れる という以上に 電位差があるところを流れること
ここでもやはり、電気は、水が高低差があると低いほうに流れるように、電圧に少しでも差があればそのスキ間に流れ込んでいく。
当たり前のようで、わかっていそうで、わかりにくいところだと思います。
電位差を流れる電気
一見、間違った回路のようですが、このような回路を考えてみます。
5V電源に240Ωの抵抗と赤色LEDを入れた回路に
加えて、反対向きに1.5Vの乾電池を入れました。
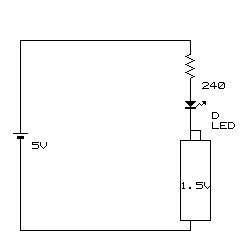
一見すると
5V電源の+から → 1.5V乾電池の+へ流れ込む
ような回路になっています。
なぜなら、電気は電位差を流れるから、という例にもなります。(これは実用回路ではないので実験的に作っています)
この回路では
- LEDの電圧は、普通に乾電池が無い場合と、どう違うか?
- LEDには実際何ボルトの電源をつないだのと同じコトになるか?
計算で考えるほうがわかりやすいような回路ですね。
上の例のホイーストンブリッジ回路の例では

B点(8V)
↓
A点(5V)
となり B点→A点 へ流れます。
3Vの電位差を伝わって流れました。
この回路は

5V → 1.5V の電位差を流れていることになります。
固定観念のように マイナス極 へしか流れ込まないようなイメージになってしまいますが、
回路の中身では 抵抗に挟まれた間などを通り、いろいろな電位差をつたってどんどん低い方へと流れ、グランドにたどり着く。
それで電気は電位差を流れるという理解から、また最初にもどり話の輪をつなげたいと思います。
- twtter
- google+
- hatena

